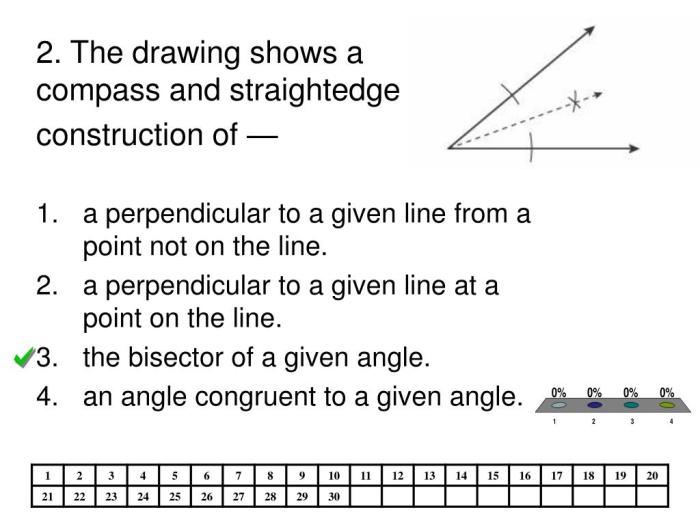
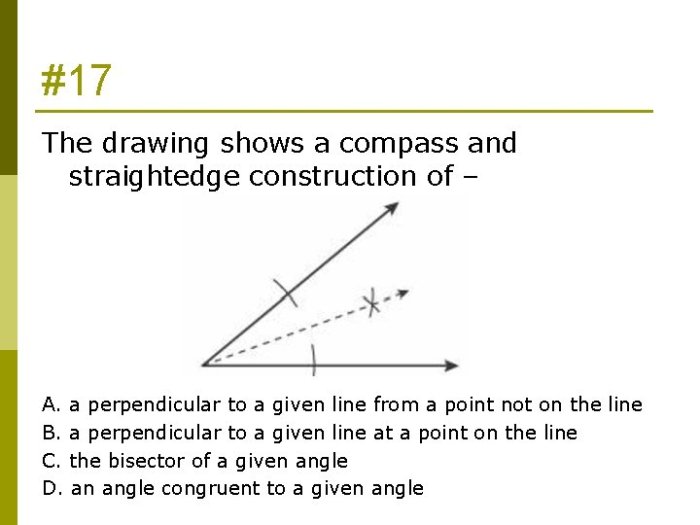
The drawing shows a compass and straightedge construction of various geometric shapes and constructions, providing a comprehensive guide to the fundamental principles and applications of these essential tools in geometry. This article delves into the historical significance, basic constructions, advanced constructions, applications, and mathematical principles behind compass and straightedge constructions, offering a thorough understanding of their role in shaping the world around us.
1. Introduction

Compass and straightedge constructions are geometric constructions that use only a compass and a straightedge. They have been used for centuries to solve a variety of geometric problems, and they continue to be an important tool in geometry today.
The compass is used to draw circles and arcs, while the straightedge is used to draw lines. By combining these two tools, it is possible to construct a wide variety of geometric shapes, including triangles, squares, circles, and polygons.
Compass and straightedge constructions have a long history, dating back to the ancient Greeks. The Greek mathematician Euclid wrote a book called “The Elements” in which he described a number of compass and straightedge constructions. This book was very influential in the development of geometry, and it is still used today as a textbook for geometry students.
2. Basic Constructions: The Drawing Shows A Compass And Straightedge Construction Of
There are a number of basic compass and straightedge constructions that are used to construct common geometric shapes. These constructions include:
- Constructing a line segment:To construct a line segment, first place the compass point at one end of the line segment and draw an arc. Then, without changing the compass setting, place the compass point at the other end of the line segment and draw another arc.
The two arcs will intersect at two points. Draw a line through these two points to construct the line segment.
- Constructing a circle:To construct a circle, first place the compass point at the center of the circle and draw an arc. Then, without changing the compass setting, place the compass point on the circumference of the circle and draw another arc. The two arcs will intersect at two points.
Draw a line through these two points to construct the circle.
- Constructing a perpendicular bisector:To construct a perpendicular bisector, first draw a line segment. Then, place the compass point at one end of the line segment and draw an arc that intersects the line segment at two points. Do the same thing at the other end of the line segment.
The two arcs will intersect at a point that is the midpoint of the line segment. Draw a line through this point and the midpoint of the line segment to construct the perpendicular bisector.
- Constructing an angle bisector:To construct an angle bisector, first draw an angle. Then, place the compass point at the vertex of the angle and draw an arc that intersects the two sides of the angle. Do the same thing on the other side of the angle.
The two arcs will intersect at a point that is on the angle bisector. Draw a line through this point and the vertex of the angle to construct the angle bisector.
3. Advanced Constructions
In addition to the basic constructions, there are also a number of advanced compass and straightedge constructions that can be used to construct more complex geometric shapes. These constructions include:
- Constructing a regular polygon:To construct a regular polygon, first draw a circle. Then, divide the circle into n equal parts, where n is the number of sides of the polygon. To do this, place the compass point at the center of the circle and draw an arc that intersects the circle at two points.
Then, without changing the compass setting, place the compass point at one of the points of intersection and draw another arc that intersects the circle at another point. Repeat this process until you have divided the circle into n equal parts.
Finally, draw lines connecting the points of intersection to construct the regular polygon.
- Constructing a triangle given its side lengths:To construct a triangle given its side lengths, first draw a line segment that is equal to the length of the longest side of the triangle. Then, place the compass point at one end of the line segment and draw an arc with a radius equal to the length of the second side of the triangle.
Do the same thing at the other end of the line segment with a radius equal to the length of the third side of the triangle. The two arcs will intersect at two points. Draw lines connecting these two points to the end of the line segment to construct the triangle.
- Constructing a triangle given its angles:To construct a triangle given its angles, first draw a line segment. Then, place the compass point at one end of the line segment and draw an arc that intersects the line segment at two points. Do the same thing at the other end of the line segment.
The two arcs will intersect at a point that is the vertex of the triangle. Draw lines connecting this point to the ends of the line segment to construct the triangle.
- Constructing a square root using a compass and straightedge:To construct a square root using a compass and straightedge, first draw a line segment that is equal to the length of the number you want to find the square root of. Then, place the compass point at one end of the line segment and draw an arc that intersects the line segment at two points.
Do the same thing at the other end of the line segment. The two arcs will intersect at a point that is the square root of the number.
4. Applications of Compass and Straightedge Constructions
Compass and straightedge constructions have a wide variety of applications in architecture, engineering, art, and design. Some of these applications include:
- Architecture:Compass and straightedge constructions are used to design buildings and other structures. For example, architects use compass and straightedge constructions to create blueprints for buildings, which show the dimensions and layout of the building.
- Engineering:Compass and straightedge constructions are used to design machines and other devices. For example, engineers use compass and straightedge constructions to create blueprints for bridges, which show the dimensions and layout of the bridge.
- Art and design:Compass and straightedge constructions are used to create works of art and design. For example, artists use compass and straightedge constructions to create geometric patterns and designs.
5. Mathematical Principles
Compass and straightedge constructions are based on a number of mathematical principles. These principles include:
- The Euclidean postulates:The Euclidean postulates are a set of axioms that define the basic properties of geometry. These postulates include the following:
- A straight line can be drawn from any one point to any other point.
- A circle can be drawn with any radius and any center.
- All right angles are equal to each other.
- The Pythagorean theorem:The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides.
- The principle of superposition:The principle of superposition states that two geometric figures can be superimposed on each other if and only if they are congruent.
FAQ Explained
What are the basic constructions using a compass and straightedge?
The basic constructions using a compass and straightedge include constructing a line segment, a circle, a perpendicular bisector, and an angle bisector.
How are compass and straightedge constructions used in architecture?
Compass and straightedge constructions are used in architecture to create precise geometric shapes and designs, such as circles, arches, and regular polygons, which are essential for structural integrity and aesthetic appeal.
What are the limitations of compass and straightedge constructions?
Compass and straightedge constructions have limitations, such as the inability to trisect an angle or construct a regular heptagon. These limitations stem from the fundamental properties of Euclidean geometry and the tools used.